Ancient to Modern Mathematics (Part 2)

Continuing from my previous article,…… ancient mathematics (part 1). Previously we talked about Babylonian, Egyptian, Greek, and Roman mathematics. In this article, we will talk about Indian Mathematics, Islamic Mathematics and 16^th-18^th century Mathematics. (Article continues below)

Indian Mathematics: Indian Mathematics was very developed in mathematics. In the early 8^thcentury BCE before the Pythagoras, a textbook found known as “Sulba Sutras.” This book contains the geometric solution for linear equations also for the quadratic equation with a single unknown variable and also gives the accurate figure of the Square Root of ‘2’. The answer in that book was 1.4142156, it is correct up to 5 decimal places.

Indians did a remarkable development in mathematics. Around the 9^thcentury, Indians used a circle with a dot in the middle as a notation of zero(0). There was a great mathematician named Brammagupta, used this zero as a number in counting. And Brahma Gupta made a new rule for calculating with zero numbers such as 1+0=1, 1-0=1, 1*0=0. Brammagupta also created a new rule for negative numbers and noticed that a quadratic equation has two possible answers.

There was another great mathematician in India around the 12^thcentury named Bhaskara II, he made clear the misunderstanding about the 1/0. As he stated, if we divide 1 by half, then we get two, 1 / 0.5=2, similarly, 1/0.333=3 which means dividing 1 by smaller number making a more significant number. So 1/0 will make the most larger number which is undefined means infinity, so he marked it with this sign1/0= ∞(infinity). Indians were also aware that pie(π) is an irrational number.

Islamic Mathematics: Persia, North Africa, Central Asia, parts of India were the base of The Islamic Empire, and they made remarkable contributions in mathematics. They could adopt both Indian and Greek mathematics.

They started using geometric drawings to decorate their construction. The Holy Qu’ran, the complete guideline for humanity, encouraged them to gain knowledge. Muslims inspired by their holy Quran and start gaining knowledge. That's why The 9^thto 15^th centuries is called the golden age of Islamic science and mathematics. They started translating all the great Greek and Indian’s mathematical and astronomical works into Arabic.

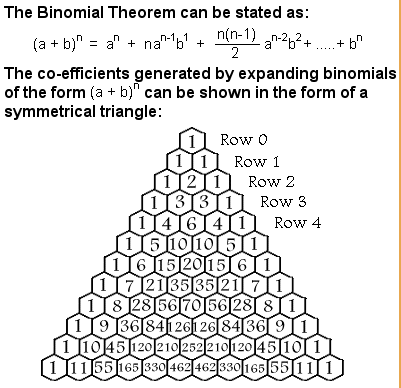
Muhammad ibn Musa Al-Khwarizmi was a well-known Persian mathematician of the 9^th century. He was a director of House of Wisdom. His important contribution was among all the numerical system Khwarizmi chose the Hindu numerical system (1-9 and 0) for their official works. Later this was adopted by the whole Islamic world as well as Europe. His principal works on mathematics were on the fundamental algebraic methods of “reduction” and “balancing” and solve the polynomial equation of second degree. There was another mathematician in the 10^th century named Al-Karaji proved binomial theorem using mathematical induction.

In the 13^th century, a Persian, scientist, mathematician, and astronomer Nasir Al-Din Al-Tusi was the first man who treated Trigonometry as the different branch of mathematics. He was an initiator of spherical Trigonometry in mathematics. One of his great works was the discovery of sine law ^a⁄_(sin_A₎= ^b⁄_(sin_B₎= ^c⁄_(sin_C₎.

There were more contributions by the Islamic empire, and in the 14^thto 15^thcentury by the ottoman empire Islamic mathematics became more strengthful and further improvement diverted to Europe.

16^th-18^thMathematics: Europe made tremendous development in all the sectors of science mathematics, physics, chemistry, astronomy, etc. In this period, many greatest scientists and mathematicians were born such as Copernicus, Galilei, Tycho Brahe, Johannes Kepler, John Napier, Pierre Simon Laplace, Isaac Newton, Gauss, Leibniz, Rene Descartes, Blaise Pascal, etc. It is impossible to finish writing here about all of their works, so here we are giving a short description of that era.

Early Galileo, Tycho Brahe, and Johannes Kepler tried to make a revolutionary discovery of the Solar system. Then the invention of the logarithm by the Jhon Napier help in some problematic calculations in astronomy. This invention also helped Kepler and newton to perform their complex calculations

the logarithm is the inverse function to exponentiation. That means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number x

For example, the base 10 logarithm of 100(log₁₀ 100) is =2. Because 10² = 100.

Marsanne is remembered for his invention of Mersenne prime-

prime numbers that are one less than a power of 2 for example3 (2²-1), 7 (2³-1), 31 (2⁵-1), 127 (2⁷-1), 8191 (2¹³-1), etc.

Rene Descartes was the inventor of Cartesian co-ordinate. This invention provided a new way to think and imagine mathematics. His invention work as a foundation of calculus and later multi-dimensional geometry.

Newton and the German philosopher and mathematician Leibniz completely changed, revolutionized mathematics also physics, economics astronomy by their invention of Calculus with two operation Integration and differentiation. Though there has a debate about who invented calculus. But probably newton developed his works before Leibniz does, but Leibniz published his works first. Nowadays, it doesn’t matter who invented first; we used extensively in our everyday engineering to astronomy to medicine to economics. Newton has other works of an area in mathematics. He generalized the binomial theorem and the theory of finite difference and the use of the finite power series.

The period of the 18^th century in Basel of Switzerland, was genuinely dominated by one family; that family was Bernoulli’s family; they bosted the mathematics for three-generation especially the brothers Jacob and Johann. They focused on developing the Leibniz's infinitesimal calculus known as “calculus of variation.”

Another mathematician who was from Basel named Euler, but he couldn’t illuminate there because of Bernoulli's family. So he spent more his time abroad and proved many theorems, established some new methods such as every integer greater than 5 can be expressed as the sum of three primes(Goldbach Conjecture) etc.another important mathematician De Moivre who is widely known for his formula (cosx + isinx)ⁿ = cos(nx) + isin(nx) which is known as the bridge formula for trigonometry and the complex number. He also generalizes the newton’s binomial theorem and makes into multinomial theorem.

Recommended reading: