From a pianist and cello player to a prominent scientist in modern physics and quantum physics. The famous physicist Max Born (German physicist and mathematician) described Max Planck as "deeply influenced by the traditions of his family and people, a zealous patriot, proud of the greatness of Germany's history, and a Prussian conscious of his attitudes towards the state."

The famous physicist did not enter physics to discover new things, according to what he said when he told his professor who told him that everything was discovered at that time in terms of physics. The reply was, "I don't want to discover new things. All that I want is an understanding of the basics of physics."
Yes, this is what the man who later won the Nobel Prize said. So If you see yourself as not being suitable to discover new things in physics, then this is most likely your chance to win a Nobel Prize! (article continues below)

So let's get to know who Max Planck is and how his life went?
His childhood
On April 23, 1858, in the city of “Kiel” in Germany, Max Karl Ernst Ludwig Planck was born into an ancient German family, as his father worked as a professor of law at the University of Kiel while his grandfather and his father’s grandfather worked as a professor of theology. So he was from a family that combined science and religion.
Later, his family moved to Munich, where his interest in physics began to emerge, along with his studies in mathematics, mechanics and astronomy at school.[1]


Music or physics?
Although he was from a family interested in theology and law, the young man was gentle feelings to the extent that it gained him the ability to compose music and operas. He was certainly good at beautifully playing the piano and cello.
But he did not continue to do so; rather, he took the opposite direction. What if Planck had continued as a musician? Would we have had another Beethoven?

Planck chooses physics
Max preferred to study physics over music; he joined the University of Munich in 1874 and was educated by great scientists such as Helmholtz, Kirchhoff and others.
A year later, he decided to focus on theoretical physics, and then submitted a thesis on heat theory, to work after that as a lecturer at the University of Munich, but without a salary.
He hoped to work as a professor at the university, and indeed his wish was fulfilled, but after five years and at the University of Kiel, not at the University of Munich, he worked as an assistant professor in the Department of Theoretical Physics in 1885. After that, he continued to work on the theory of heat and entropy.
Then he worked as the heir to his great professor Kirchhoff at the University of Berlin, to which he had transferred, where he worked as a professor of classical physics, and that was in 1889.

Black Body radiation
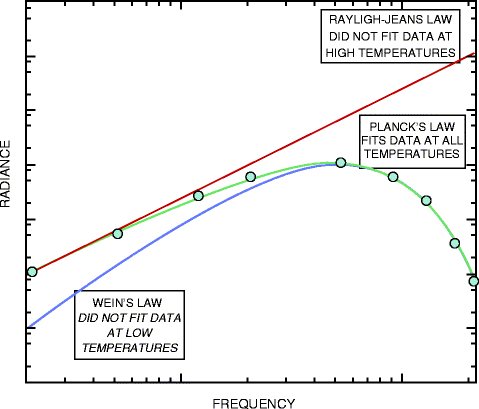
The black body is defined as an ideal, imaginary object that scientists aim to study theoretically to reach an explanation and understand the radiation of other objects found in reality. Like other scholars of his time, Planck became interested in the subject of the black body and the rays of the black body, and that was in 1894.
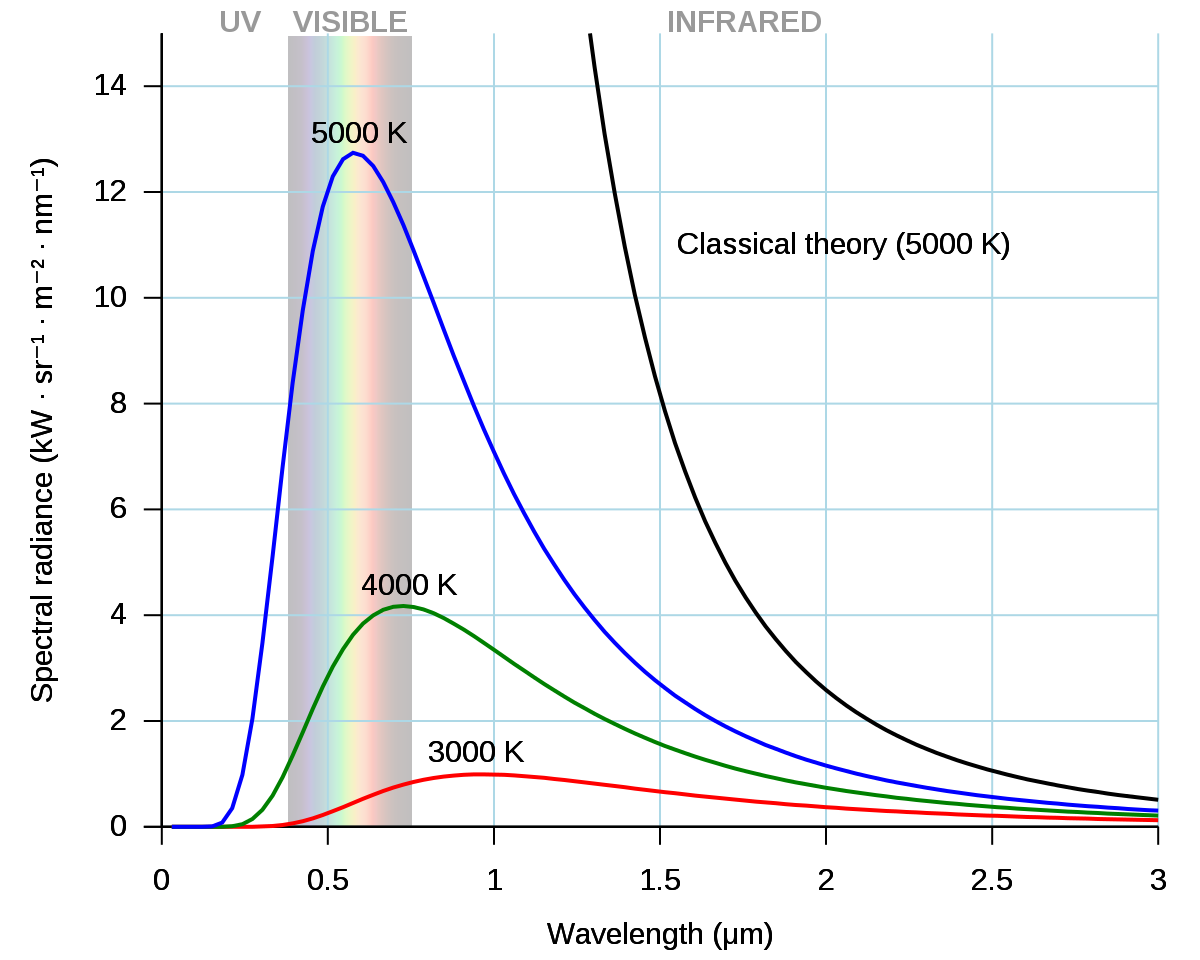
Planck's interest was in his attempt to understand the relationship of the intensity of radiation from the black body to a certain frequency and wavelength, or in the sense of the color of the light emitted by it, in the case of visible light, and its relationship to the temperature of the black body.
His attempts resulted in the issuance of his first theories about the black body, which was in the year 1900, but unfortunately, they were not completely correct, and Planck was aware of that.
But despite its inaccuracy, part of what the previous musician realized had a great impact later on the future of physics, as he noticed the energy emitted in the form of equal quanta and not in the form of a continuous wave, as classical physics says. These quanta possess specific qualities, as they are equal Frequently, multiples of a constant, later called the "Planck constant."[2]
Planck and Einstein [3]
Planck's theory was not viewed with interest by scientists, but with the passage of time, the matter gradually changed, as the quantum idea proposed by Planck was able to explain many things that were difficult to explain through classical physics.
For example, in the year 1905, Einstein was presenting his practical explanation for the photoelectric phenomenon. His explanation was as follows: the energy of light is not continuous wave energy, but rather it is divided into equal quantities of energy known as photons. If you want to calculate the energy of these photons, you will be obliged to use the constant proposed by Planck.
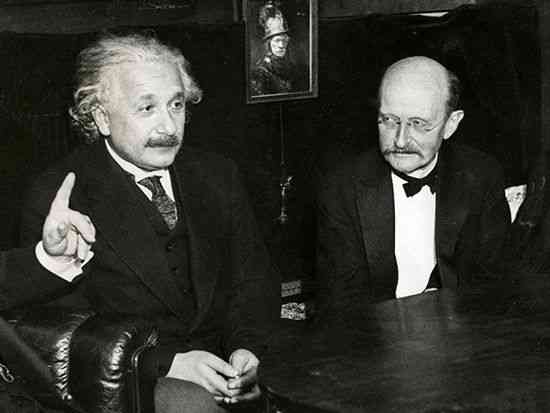
Depending on the fundamental physical constants such as the Coulomb constant, the Boltzmann constant, the velocity of light in vacuum, and the gravitational constant, the Planck constant was confirmed as the fundamental energy quantum Planck units. It was calculated as Planck time, Planck length, and Planck temperature.
As a result, a close friendship was strengthened between the two geniuses, and they spent a long time playing Planck on the piano and Einstein playing the violin. Because of Planck's strong support for Einstein's theory of relativity initially, it was good at making them close friends.

Planck became president of the German Society of Physicists in 1905 and was keen to make Einstein's theory firmly heard by all physicists.
Einstein won the Max Planck Medal as a prize, and Einstein says of their friendship:
Perhaps that friendship was the main factor in changing the future of physics completely, as it had a role in Max Planck's resilience in the face of the troubles he faced in his life.
Max Born describes them:
It is difficult to imagine two men more different than they are, for Einstein is a global citizen who has little to do with those around him, independent of the emotional background of the society in which he lives. As for Planck, he is deeply influenced by the traditions of his family and people, and a zealous patriot, proud of the greatness of Germany's history, and a Prussian conscious of his attitudes towards the state.”
The Tragic End
Planck was one of the four permanent presidents of the Prussian Society of Sciences when misfortunes began to follow him, and that was with the beginning of World War I. He had declared at the beginning of the war his support for it, but he changed to the opposition after that, and in that war, three of his sons died because of War is direct and because of disease.
The war ended, and the Nazis came to power in 1933, and Planck was 74 years old. In secret, Planck strongly opposed the ideas of the party and had a hand in maintaining some of the Jewish scholars in their positions in universities, which caused his severe hostility by the German scholars' movement(Deutsche Physik), which Heisenberg was one of its members.

Due to the continued harassment of him by the Nazis, Planck resigned from the presidency of the Borussia Society of Sciences, and the Nazis stood against any access to any other position.
In the year 1944, Hitler was subjected to a failed assassination attempt, and Erwin (son of Planck) was one of the accused, and he was convicted and later executed, which had a great impact on Planck in a painful way.
The matter did not stop at this point, as it happened that Planck's house in Berlin was bombed and was completely destroyed, which prompted him to migrate to the countryside without settling in it. Afterward, he lived his life traveling, giving lectures on physics and religion in different countries of the world.
His death
In fact, during our research on how Max died, we did not find anything certain. Some say that he died of suicide because of his disbelief and rejection of his hypotheses that were later proven after his death, and others say that he died of a heart attack, and some say that it is due to brain retardation.

THE END
Finally, after the black end that Planck experienced in his life, we can understand why he wrote these words:
“No man was born with a legal right that gives him happiness, success, and prosperity in life. Therefore, we must accept every decision of God’s providence, every hour of happiness, as an unearned gift that imposes a commitment on us. As for the only thing that we may claim to be ours with absolute assurance, the greatest good, What no power in the world can take from us, which can give us lasting happiness more than anything else, is the integrity of the soul, which is manifested in the conscientious performance of our duty." [4]
Recommended reading:

Sources:
[1]Roger H. Stuewer/Professor Emeritus of the History of Science and Technology, University of Minnesota, Minneapolis. (LAST UPDATED: Sep 30, 2020) "Max Planck German physicist" , retrieved (2/10/2020)
https://www.britannica.com/biography/Max-Planck
[2]PATRICK J. KIGER(DEC 10, 2019)"What Is Planck's Constant, and Why Does the Universe Depend on It?" ,retrieved (2/10/2020)
https://science.howstuffworks.com/dictionary/physics-terms/plancks-constant.htm
[3]Oxford Academic (Oxford University Press)/channel on youtube (Jul 9, 2015), "The friendship between Max Planck and Albert Einstein" , retrieved (2/10/2020)
https://www.youtube.com/watch?v=nTaD3YA5htc
[4]Al Jazeera (23/4/2017) , "This is how Max Planck spoke" ,retrieved (2/10/2020)
https://www.aljazeera.net/midan/miscellaneous/science/2017/4/23/هكذا-تحدث-ماكس-بلانك



