Calculus is the study of Change in mathematical terms, sometimes it is called "mathematics of change." It is a branch of mathematics through which we can easily explain the path of change of one variable relative to another. We know mathematics may have started a long time ago, and it has been improving from the beginning. But if you ask where the birth of modern mathematics is? If the answer is calculus, many scholars may agree. The origin of this new section of mathematics was developed by two famous mathematicians named Sir Isaac Newton and Leibniz. (Article continues below)

They were the first to introduce the concept of this modern mathematics section (calculus) with a combination of algebra, geometry, and trigonometry. Now, in the 21st century, it would never be possible to imagine mathematics or theoretical physics without calculus. Basically, calculus is of two types:
- Differentiation
- Integration
Differentiation
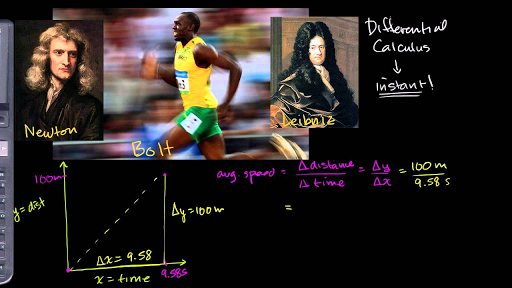
If y = f (x) is a function, then with the help of differentiation, we can find the maximum and minimum values of variable y with respect to x (for any value of x). let's see differentiation from different points of view. In physics, many actions depend on time.
The equations which are based on time need the help of differentiation to solve them, such as: In a line, the displacement in a point is given, Let t=3; X (t) = 16t ^ 2 + 16t + 32
Then we can determine its velocity with the help of differentiation calculation, X '(t) = 32t + 16And can diagnose acceleration, X ”(t) = 32If we narrate these mathematical terms, we can say: On 3rd second the displacement was x= 224m. on second line, after differentiation; we can say the velocity X ' = 112 m/s. and in the last mathematical line (after two-time differentiation) says, the acceleration of this is 32 m/s^2.

Differentiation is the weapon for calculating the slope of any line; y = f (x) = mx + b, [the real numbers m and b], and the slope will be m = Δy / Δx where the symbol Δ is (the capital letter for the Greek letter Delta). m = Δy / Δx; this symbol means how much change of variable y with respect to variable x. when Δx is so close to zero (o), at that time, we write m= dy/dx.
Integration
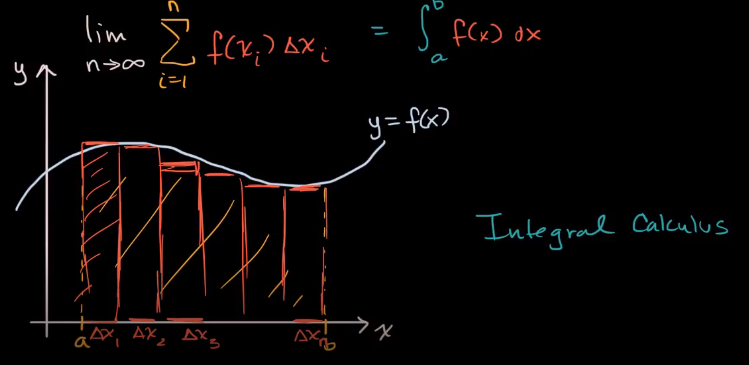
This section of calculus is entirely opposition term (also process) of differentiation. If a real variable is an interval [a, b] between x and the number line, the exact equivalent of the function f.The term integral may also refer to the concept of indefinite integral.
Isaac Newton and Gottfried Leibniz both published the fundamental theorem of calculus separately. If f is an integral function in spacing [a, b], and f is the indefinite equivalent of f, then f is the definite equivalent of the calculus founders imagine integration as a square of a tiny width as an infinite sum. Bernhart Riemann gave a mathematical definition of proper integration. According to him, "this is a boundary-method, in which the area is measured by breaking a curved-enclosed region into a thin vertical slab-region."
In the early nineteenth century, there became a more sophisticated concept, where function type and generalization of domains became. A line integral is defined for the function of two or three variable variables, and the difference [a, b] is replaced by a fixed curve of that function connected at two points on the plane or in space. In a surface integral, The curved three-dimensional space is replaced by a piece surface. Integrals All these generalizations came from the demands of the first physics, and they played an important role in creating many physical forms, including significant in electrodynamics.
Recommended reading:

Reference:
[1] https://online-learning.harvard.edu/course/calculus-1?delta=0



